
感受
考试感觉有手就行,20分钟写完,结果就96,乐

绪论
逻辑结构
1. 线性结构 1:1
2. 树形结构 1:n
3. 图结构 m:n
4. 集合结构 没啥关系
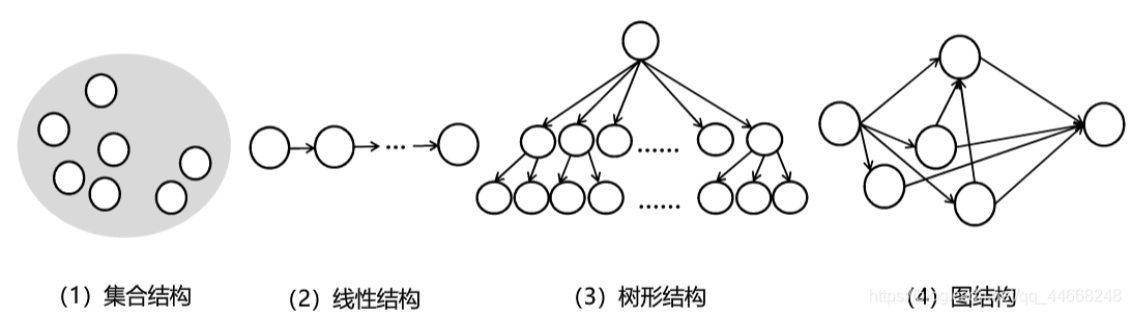
分成两类:线性数据结构与非线性数据结构(废话)
存储结构
1. 顺序存储结构 依次存储
2. 链式存储结构 连续的或不连续的存储空间
算法时间复杂度
$$O\left(1\right)<O\left(\log_2n\right)<O\left(n\right)<O\left(n\log_2n\right)<O\left(n^2\right)<O\left(n^3\right)<O\left(n!\right)<O\left(n^n\right)$$
例子:
1
2
3
4
| do{
...
i=k*i;
}while(i<=n)
|
时间复杂度:$O\left(\log_kn\right)$
1
2
3
4
5
| while(n>=f(y))
{
...
y++;
}
|
时间复杂度:$O\left(f^{-1}\left(n\right)\right)$
线性表
顺序存储结构
1
2
3
4
5
6
| typedef struct seqList
{
int n; // 元素个数
int maxLength; // 最大长度
ElemType *element; // 数组头指针
}
|

插入
1
2
3
4
5
6
7
8
9
10
11
12
13
| Status Insert(SeqList *L, int i, ElemType x) //L:线性表 i:待插入下标 x:待插入元素
{
int j;
if(i < -1 i > L->n-1) //下标i越界
return ERROR;
if(L->n == L->maxLength) //顺序表存储空间已满
return ERROR;
for(j = L->n-1 ; j>i ;j--)
L->element[j+1] = L->element[j]; //从后往前逐个后移
L->element[i+1] = x; //新元素插入
L->n++; //元素个数+1
return OK;
}
|
时间复杂度:$ O\left(n\right) $
删除
1
2
3
4
5
6
7
8
9
10
11
12
| Status Delete(SeqList *L, int i) //L:线性表 i:待删除下标
{
int j;
if(i < -1 i > L->n-1) //下标i越界
return ERROR;
if(!L->n) //顺序表为空
return ERROR;
for(j=i+1 ; j < L->n ;j++)
L->element[j-1] = L->element[j]; //从前往后逐个前移
L->n--; //元素个数-1
return OK;
}
|
时间复杂度:$ O\left(n\right) $
查找
1
2
3
4
5
6
7
| Status Find(SeqList L,int i,Element *x)
{
if(i<0 i > L.n-1)
return ERROR;
*x = L.element[i];
return OK;
}
|
时间复杂度:$ O\left(1\right) $
单链表
1
2
3
4
5
6
7
8
9
10
| typedef struct node
{
ElemType element ; //结点的数据域
struct node *link;//结点的指针域
}Node;
typedef struct singleList
{
struct node *first; // 表头结点
int n; // 元素个数
}SingleList;
|

插入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| Status Insert(SingleList *L, int i, ElemType x) //L:线性表地址 i:插入下标 x:插入值
{
Node *p, *q;
int j;
if(i<-1 i > L->n-1) // i越界
return ERROR;
p = L->first;
for(j=0 ; j<i ;j++) //p从头结点开始遍历
p = p->link;
q = malloc(sizeof(Node)); //给待插入结点申请空间
q->element = x; // 待插入结点数据域赋值
if(i>0) // 插入位置不是头结点
{
q->link = p->link; // q指针指向p下一个结点
p->link = q; // p结点指针指向q
}
else
{
q->link = L->first; // q指针指向原头结点
L->first = q; // L头结点变为q
}
L->n++; // 表长++
return OK;
}
|
删除
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| Status Delete(SingleList *L, int i) //L:线性表地址 i:待删除下标
{
Node *p,*q;
int j;
if(i<0 i > L->n-1) // i越界
return ERROR;
if(!L->n) // 链式表为空
return ERROR;
p = L->first;
for(j=0 ; j < i - 1 ; j++) //p 遍历到待删除位置
p = p->link;
if(i==0) // 删除的是头结点
L->first = L->first->link; //L头结点为原头结点指针指向的结点
else //正常的结点
{
q = p->link; //q为p所指向的结点
p->link = q->link; // p指针指向结点为q指针指向的结点
}
free(q); // 释放被删除q的空间
L->n--; // L元素个数-1
return OK;
}
|
查找
1
2
3
4
5
6
7
8
9
10
11
12
| Status Find(SingleList L, int i, Elemtype *x)
{
Node *p;
int j;
if(i<0 i>L.n-1) // i越界
return ERROR;
p = L.first;
for(j=0 ; j<i ;j++) // p从头遍历
p = p->link;
*x = p->element; // x赋值
return OK;
}
|
带表头单链表
1
2
3
4
5
| typedef struct headerList
{
struct Node *head; //定义表头
int n; //元素个数
}HeaderList;
|
初始化
1
2
3
4
5
| void Init(HeaderList *L){
L->head=(Node*)malloc(sizeof(Node));
L->head->link=NULL;
L->n=0;
}
|
(单)循环链表

也可以带表头
双向链表
1
2
3
4
5
6
| typedef struct Node
{
ElemType element; // 数据域
struct Node *llink; //左指针域
struct Node *rlink; //右指针域
}DuNode,DuList;
|

插入
1
2
3
4
| q->llink = p->llink; // q左指针指向p左指针指向的结点
q->rlink = p; // q右指针指向p结点
p->llink->rlink = q; // p左指针指向的结点(即p原左结点)右指针指向q结点
p->llink = q; // p左指针指向q
|

删除
1
2
3
| p->llink->rlink = p->rlink; // p的左结点直接指向p的右结点
p->rlink->llink = p->llink; // p的右结点直接指向p的左结点
free(p); // 释放p
|

线性表优劣比较
顺序表
单链表
带表头的链表
循环链表
双向链表
优
查找速度$$O(1)$$
确定位置后,增删速度$$O(1)$$ 不需要估计存储长度
方便插入和删除操作的实现
从表中任意结点出发都能扫描整个链表
可快速访问直接前驱
劣
增删速度$$O(n)$$ 需要先估计存储空间
查找速度$$O(n)$$ 增删中头结点需要单独考虑
栈堆和队列
栈堆
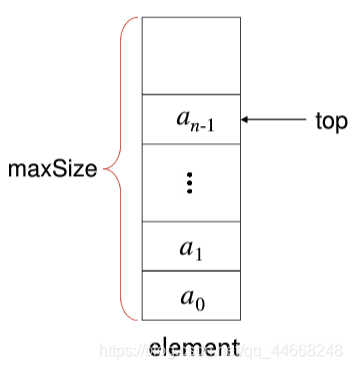
共有$$f(n)=\dfrac{C^n_{2n}}{n+1}$$种出栈顺序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| //定义
typedef struct stack
{
int top; // 栈顶位置下标,空栈为-1
int maxSize; // 栈最大容量
ElemType *element; //栈数组首地址
}
//创建
void Create(Stack *S, int mSize) //S:栈地址 mSize:最大容量
{
S->maxSize = mSize; //获取最大容量
S->element = (ElemType*)malloc(sizeof(ElemType)*mSize); //给栈申请空间
S->top=-1; //栈顶为负
}
//销毁
void Destroy(Stack *S)
{
S->maxSize = -1; //容量为负
free(S->element); //释放栈数组
S->top = -1; //栈顶为负
}
//销毁不释放
void Clear(Stack *S)
{
S->top = -1; //仅仅将栈顶归负
}
//取栈顶元素
BOOL Top(Stack *S, ElemType *x)
{
if(IsEmpty(S)) //空栈
return ERROR;
*x = S->element[S->top]; //取栈顶
return TRUE;
}
- 满栈——S->top == S->maxSize-1
- 空栈——S->top == -1
//入
BOOL Push(Stack *S, ElemType x)
{
if(IsFull(S)) // 溢出
return FALSE;
S->top++; //栈顶上移
S->element[S->top] = x; //栈顶取值
return TRUE;
}
//出
BOOL Pop(Stack *S)
{
if(IsEmpty(S)) //空栈
return TRUE;
S->top--; //栈顶下移
return TRUE;
}
|
队列
注意:教材给的a0没有数据,front所在为空,所以实际存储量maxsize-1
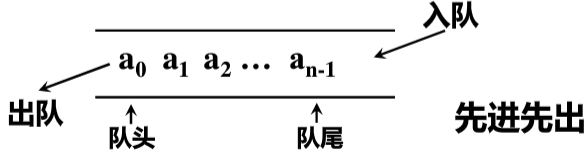
- 空队列——
front == rear
- 满队列——
(rear+1) % maxSize == font
- 队尾进1(入队)——
rear = (rear+1) % maxSize
- 队头进1(出队)——
front = (front+1) % maxSize
会假溢出,所以还是用循环队列
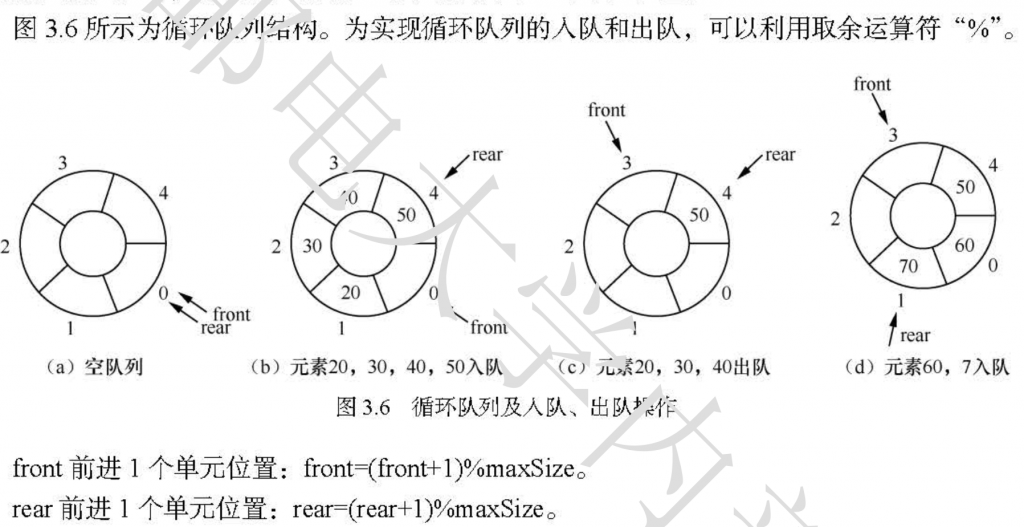
循环队列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| //定义
typedef struct queue
{
int front; //队头位置
int rear; //队尾位置
int maxSize; //队列容量
ElemType *element; // 队列数组首地址
}Queue;
//创建
void Create(Queue *Q, int mSize) //Q:队列首地址 mSize:最大容量
{
Q->maxSize = mSize; // 最大容量赋值
Q->element = (ElemType*)malloc(sizeof(ElemType)*mSize); // 为队列数组申请空间
Q->front = Q->rear = 0; // 队头队尾归零
}
//销毁
void Destroy(Queue *Q)
{
free(Q->element); //释放数组空间
Q->maxSizw = -1; //最大容积归负
Q->front = Q->rear = -1; //队头队尾归负
}
//销毁不释放
void Clear(Queue *Q)
{
Q->front = Q->rear = 0; // 队头队尾归零
}
//获取队头
BOOL Front(Queue *Q, ElemType *x)
{
if(IsEmpty(Q)) // 空队列
return FALSE;
*x = Q->element[(Q->front+1) % Q->maxSize]; // 取队头元素
return TRUE;
}
//入
BOOL EnQueue(Queue *Q, ElemType x)
{
if(IsFull(Q)) // 溢出
return FALSE;
Q->rear = (Q->rear+1) % Q->maxSize; // 队尾进1
Q->element[Q->rear] = x; // 队尾赋值
return TRUE;
}
//出
BOOL DeQueue(Queue *Q)
{
if(IsEmpty(Q)) // 空队列
return FALSE;
Q->front = (Q->front+1) % Q->maxSize; //队头进1
return TRUE;
}
|
链式队列
教材未作重点,但是了解一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| //定义
typedef struct node
{
Elemtype element; //数据域
struct node *link; //指针域
}Node;
typedef struct queue
{
Node *front; //头指针
Node *rear; //尾指针
}Queue;
//入
void Enqueue(Queue *Q, ElemType x)
{
Node *p = (Node*)malloc(sizeof(Node)); // 结点申请空间
p->element = x; // 结点赋值
p->link = NULL; // 结点指向空
Q->rear->link = p; // 队列尾指向结点
Q->rear = p; //结点作为队列尾
}
//出
void DeQueue(Queue *Q)
{
if(Q->front == NULL) // 空队列
return;
Node *p = Q->front; //结点p移动到队头
Q->front = p->link; //队头变为结点所指向的结点
free(p); //释放结点
if(Q->front == NULL) //若为空队,重置队尾
Q->rear = NULL;
}
|
后缀表达式
应该就考填空
书上是栈的方法,我们来用这个
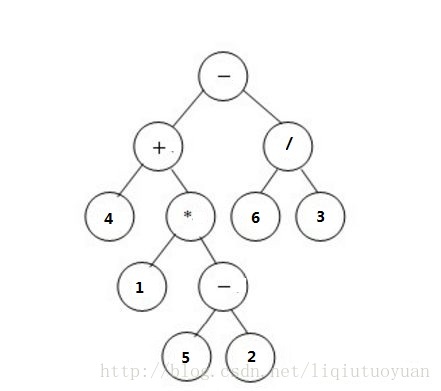
- 先序遍历(先根)是先访问当前节点,然后再遍历左子树,最后是右子树。
- 中序遍历(中根)是先遍历左子树,再访问当前节点,最后是右子树。
- 后序遍历(后根)是先遍历左子树,再遍历右子树,最后访问当前节点。
显然,逆波兰表达式为:4 1 5 2 - * + 6 3 / -
数组和字符串
数组(库)
一维数组
$Loc(a[i]) = Loc(a[0]) + i*k$
二维数组

行优先顺序地址计算

$$loc(ai)=loc(a0)+(in+j)k$$
- $k$——每个元素存储单位
- $loc(a0)$——第一个元素存储地址
- $loc(ai)$——$ai$存储地址
列优先

$loc(ai)=loc(a0)+(jm+i)k$
数组抽象数据结构(三维数组实现)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| //定义
typedef struct tdarray{
int m1, m2, m3; // 每个维度的值
int *array; //数组首地址
}TDArray;
//创建
Status CreateArray(TDArray *tdArray, int m1,int m2,int m3)
{
tdarray->m1 = m1;
tdarray->m2 = m2;
tdarray->m3 = m3;
tdarray->array = (int*)malloc(m1*m2*m3*sizeof(int)); // 申请空间
if(!tdarray->array) //申请失败
return ERROR;
return OK;
}
//下标检查(返回地址)
Status RetrieveArray(TDArray tdarray,int i1,int i2,int i3,int *x)
{
if(!tdarray.array) //数组不存在
return NotPresent;
if(i1<0 i2<0 i3<0 i1>tdarray.m1 i1>tdarray.m2 i1>tdarray.m3 ) //越界
return IllegalIndex;
*x = *(tdarray.array+i1*tdarray.m2*tdarray.m3+i2*tdarray.m3+i3); // 返回存储位置
return OK;
}
|
特殊矩阵
对称矩阵
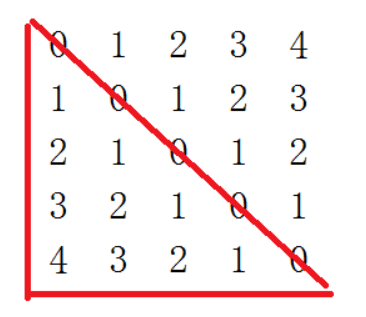
存上三角或者下三角
下三角矩阵
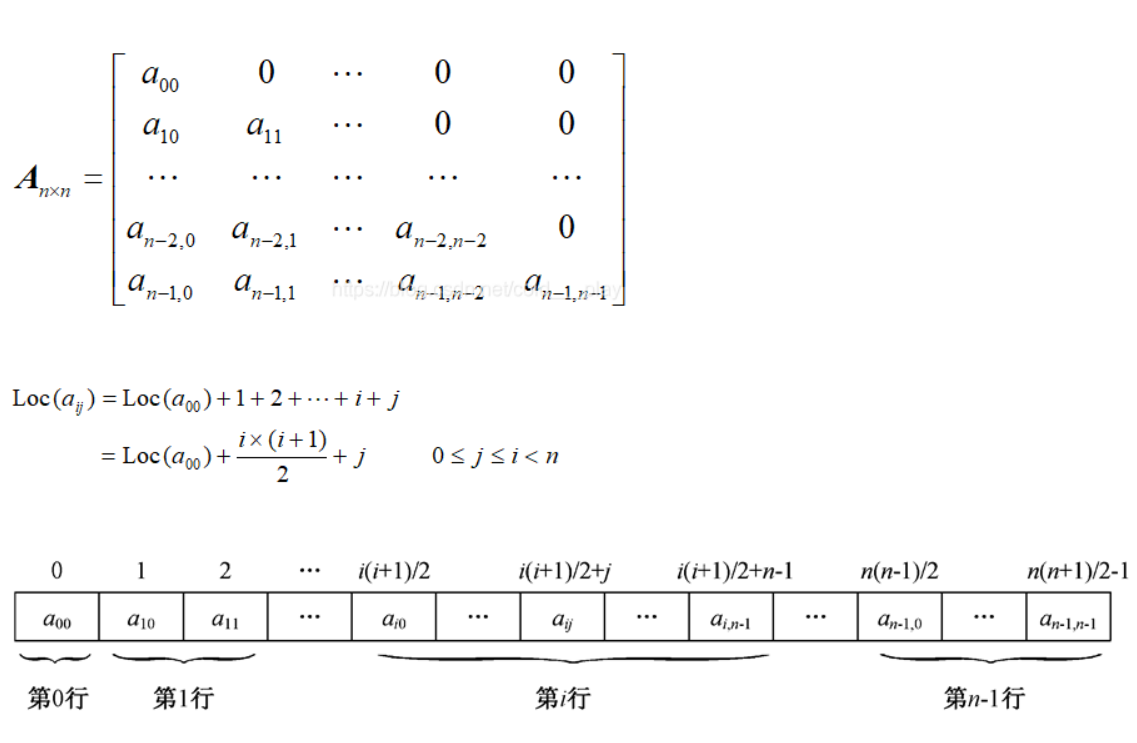
上三角矩阵

0或者其他常数放到最后一个值里面
稀疏矩阵
以三元组$<i,j,a_{ij}>$表示

1
2
3
4
5
6
7
8
9
10
| typedef struct term
{
int col,row; // 列下标,行下标
ElemType value; // 非零值
}Term;
typedef struct sparsematrix
{
int m,n,t; //m是矩阵行数,n是矩阵列数,c是非零元速个数
Term table[maxSize]; // 存储非零元的三元组表
}
|
稀疏矩阵转置算法
第一种
- 交换$i,j$
- 以$i,j$从小到大排序
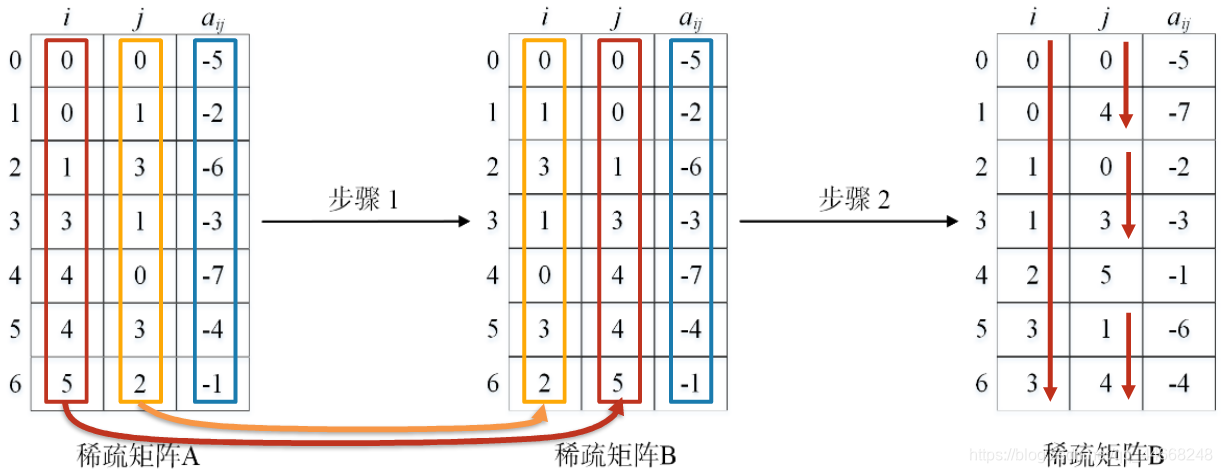
时间复杂度
- 步骤一:$O(t)$ $t$——非零元素个数
- 排序复杂度$O(t^2)$或者$O(t\times\log_2\left(t\right))$
第二种
- 找到所有$<i,0,a_{i0}>$,交换$i,j$后依次保存到稀疏矩阵$B$
- 找到所有$<i,1,a_{i1}>$,交换$i,j$后依次保存到稀疏矩阵$B$
- $……$

时间复杂度
$O(n \times t)$
快速转置算法
- 计算每列非零元素个数$num[j]$
- 计算前$j$列非零元素个数$k[j]$
1
2
3
4
5
6
7
8
9
| for(j=0;j<n;j++)
num[j] = 0;
for(i=0;i<t;i++)
num[A.table[i].col]++;
for(j=0;j<n;j++)
k[j] = 0;
for(i=1;i<t;i++)
k[i] = k[i-1] + num[i-1];
|
都是$O(t+n)$,n为矩阵的列数
1
2
3
4
5
6
| for(i = 0;i < t;i++){
int index = k[A.table[i].col]++;//先赋值再自增,是下一次的起始位置
B.table[index].col = A.table[i].row;
B.table[index].row = A.table[i].col;
B.table[index].value = A.table[i].value;
}
|
字符串
疑似不考
树和二叉树
术语
结点关系
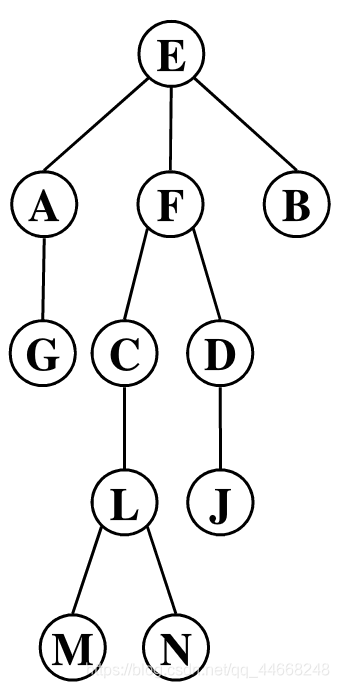
- 结点 树中的元素
E、A、F、B、G、C均为结点
- 边 根节点和子树跟之间
- 路径 从某个结点可达另一个结点
E、N间存在路径
- 双亲 该结点上连的点
A、F、B双亲是E;D双亲是F
- 孩子 该结点下连的点
E有3个孩子:A、F、B;D有一个孩子J
- 兄弟 有共同双亲的结点
A、F、B互为兄弟;C、D互为兄弟
- 后裔 子树的所有结点
C后裔为L、M、N
- 祖先 向上到根结点所有的点
L祖先为E、F、C
度
- 结点的度 结点的子树数
E:3;F:2;A:1;G:0
- 叶子 度为0的结点
B、G、J、M、N均为叶子
- 分支节点 度不为0的结点
E、A、F、C均为分支结点
- 树的度 结点度最大值
3
高度

- 结点的层次 第几层
E:1;M:5
- 树的高度 最大层次
5
有序/无序
- 无序树
 各子树顺序可交换
各子树顺序可交换
- 有序树
 各子树顺序不可交换
各子树顺序不可交换
二叉树
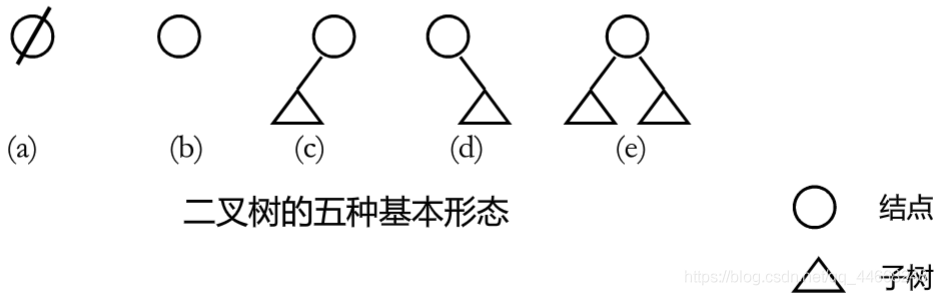
性质
- 第$i$层至多$2^{i-1}$个结点
- 高度为$h$的二叉树最多$2^{h}-1$个结点
- 包含$n$个结点的二叉树,$[log_2(n+1)]{\leq}h{\leq}n$
- 叶结点:$n_0$;度为$2$的结点:$n_2$可以得出: $n_0=n_2+1$
特殊二叉树(3种)
满二叉树
高度为$h$,且$2^h-1$结点
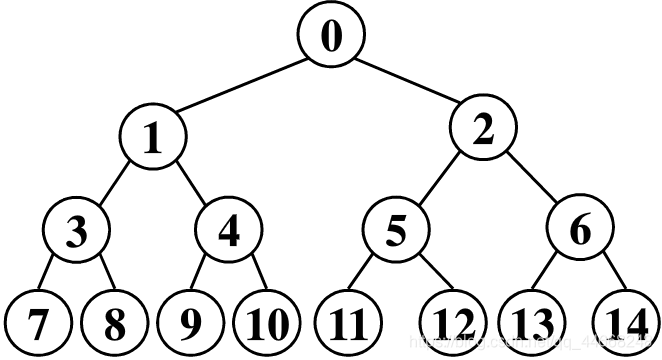
完全二叉树
- 除最下面两层度小于$2$,其他层结点度均为$2$
- 最下一层叶结点均依次集中在靠左若干位置
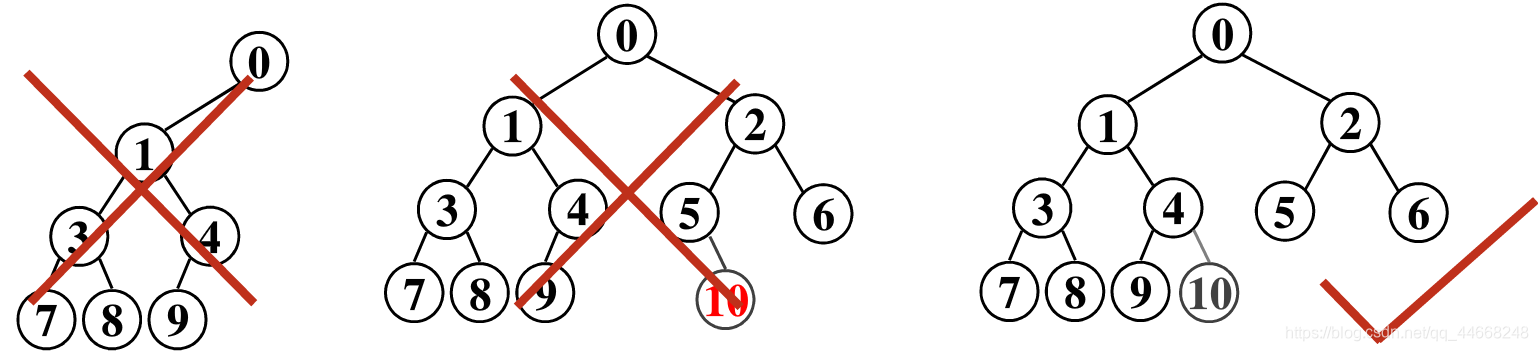
- 完全二叉树高度$h=[log_2(n+1)]$
- 由上到下、由左到右、从$0$编号根——$i=0$双亲——$[\dfrac{i-1}{2}]$左孩子——$2i+1$右孩子——$2i+2$
扩充二叉树(2-树)
- 除叶子结点,必须有两个孩子
- 仅有度$2$和$0$的结点,不存在度为$1$的结点

二叉树存储表示和部分运算
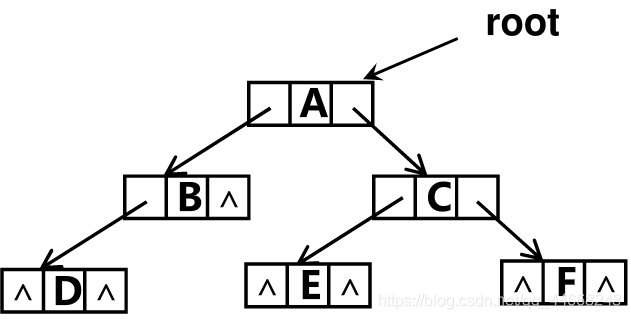
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| //定义
typedef struct btnode
{
ElemType element; // 元素内容
struct btnode *lChild; // 左孩子指针
struct btnode *rChild; // 右孩子指针
}BTNode;
typedef struct binarytree
{
BTNode *root;
}BinaryTree;
//创建空二叉树
void Create(BinaryTree *bt)
{
bt->root = NULL;
}
//创建新结点
BTNode* NewNode(ElemType x, BTNode *ln, BTNode *rn)
{
BTNode *p = (BTNode*)malloc(sizeof(BTNode)); // 申请空间
p->element = x; // 结点内容赋值
p->lChild = ln; // 左子树赋值
p->rChild = rn; // 右子树赋值
return p;
}
//返回根结点
BOOL Root(BinaryTree *bt, ElemType *x)
{
if(!bt->boot) // 空树
return FALSE;
else
{
*x = bt->root->element; // 赋值
return TRUE;
}
}
//构造二叉树
void MakeTree(BinaryTree *bt, ElemType e, BinaryTree *left, BinaryTree *right) // bt:根地址 e:根值 left:左子树 right:右子树
{
if(bt->root left==right)
return;
bt->root = NewNode(e,left->root,right->root);
left->root = right->root = NULL;
}
|
先序遍历和层次遍历
先根遍历:$O(n)$
- 先访问根结点
- 先序遍历左子树
- 先序遍历右子树
1
2
3
4
5
6
7
8
9
10
11
12
| void PreOrderTree(BinaryTree *bt)
{
PreOrder(bt->root); // 调用先序遍历函数
}
void PreOrder(BTNode *t) // 先序遍历递归函数
{
if(!t) // 树空了直接返回
return;
printf("%c",t->element); //访问根结点
PreOrder(t->lChild); // 先序遍历左子树
PreOrder(t->rChild); // 先序遍历右子树
}
|
步骤:
- 若二叉树为空,直接退出否则,初始化队列再将根结点进队
- 若队列不为空
- 获取队头结点$p$,并将队头结点出队
- 访问结点$p$中的数据
- $p$的左孩子进队
- $p$的右孩子进队
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| void LevelOrderTree(BinaryTree *tree)
{
Queue Q; // 存储BTNode结点类型指针的队列
BTNode *p;
if(!tree->root) // 二叉树为空
return;
Create(&Q, tree->root); // 初始化队列
EnQueue(&Q, tree->root); // 根结点进队
while(!IsEmpty(&Q))
{
Front(&Q,&p); DeQueue(&Q); // 获取队头结点
printf("%c",p->element); // 访问结点p
if(p->lChild) EnQueue(&Q,p->lChild); //若左孩子存在,则进队
if(p->rChild) EnQueue(&Q,p->rChild); //若右孩子存在,则进队
}
Destroy(&Q); // 销毁队列
}
|
树和森林
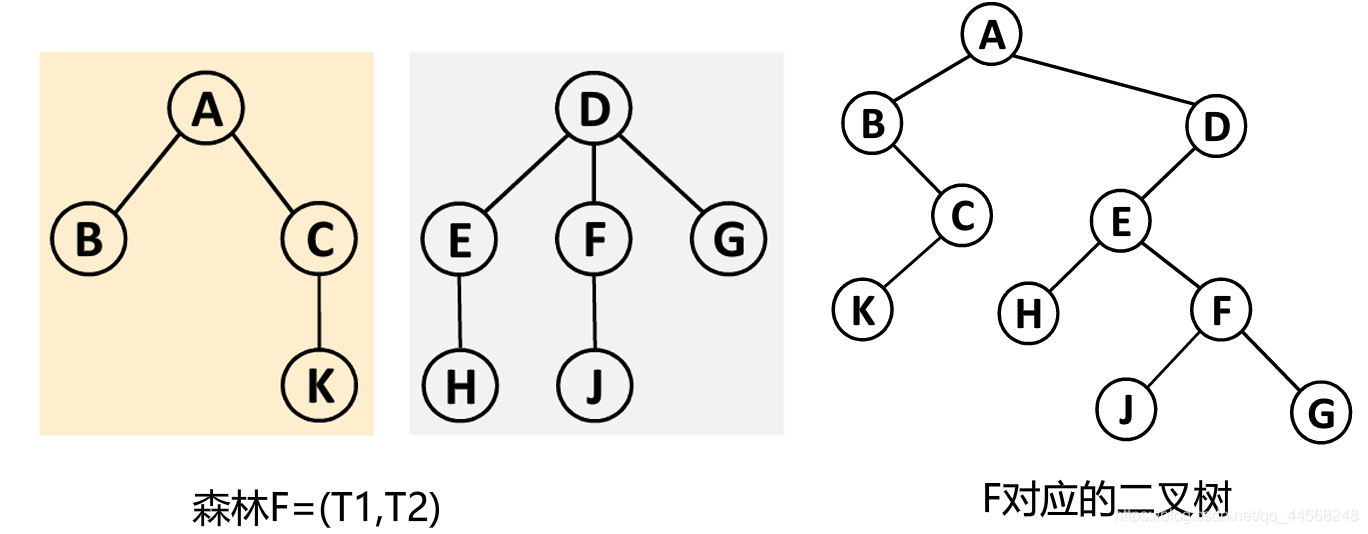
先序遍历
若森林为空,则结束
- 访问第一棵树根
- 第一棵树的根结点子树构成的森林
- 先序遍历其他树
中序遍历
若森林为空,则遍历结束;否则
- 中序遍历第一棵树的根结点的子树构成的森林
- 访问第一棵树的根
- 中序遍历其他树
后序遍历
若森林为空,则遍历结束;否则
- 后序遍历第一棵树的根结点的子树构成的森林
- 后序遍历其他树
- 访问第一棵树的根
层次遍历
- 访问第一层所有结点
- 访问第二层所有结点
- $……$
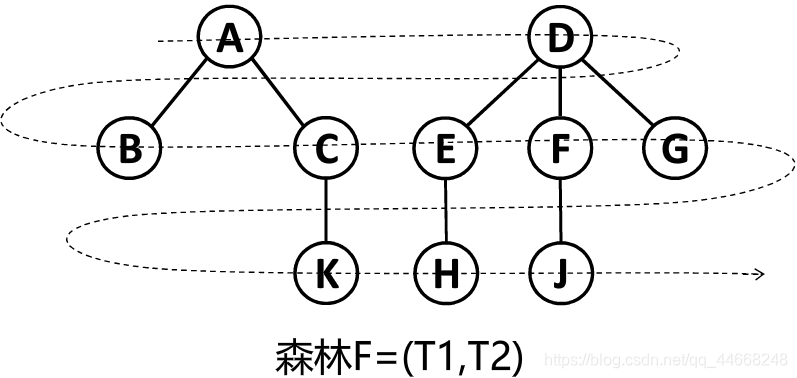
堆
最小堆
每个结点数据小于等于孩子结点
最大堆
每个结点数据大于等于孩子结点
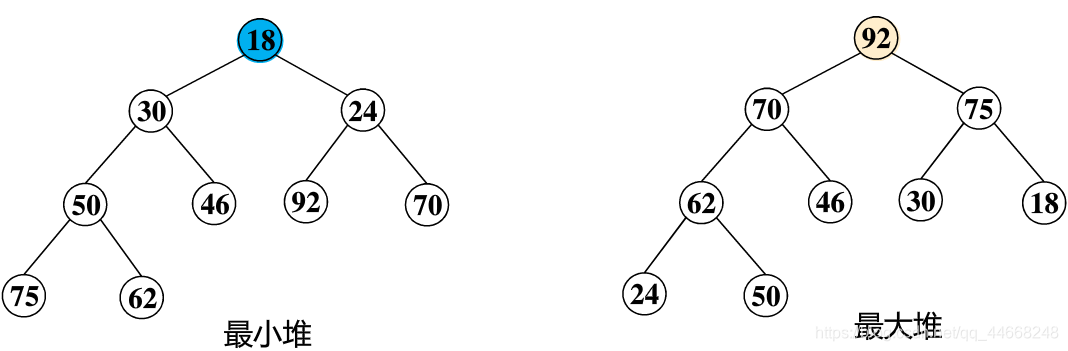
堆的判断

最小堆
$k_i{\leq}k{2i+1}$和$k_i{\leq}k{2i+2}$
最大堆
$k_i{\geq}k{2i+1}$和$k_i{\geq}k{2i+2}$
建堆运算
从最后叶子的双亲$k_{[\frac{n-2}{2}]}$反方向直到根结点$k_0$,依次对每个结点$k_i$
- 若该结点小于(大于)或等于其孩子,则结束
- 将该结点与与最小(大)孩子交换
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| //向下调整算法
void AdjustDown(ElemType heap[], int current, int border) // heap:存放序列数组 current:当前待调整序列中的位置 border:待调整序列的边界
{
int p = current;
int minChild;
ElemType temp;
while(2*p+1 <= border) // 若p不是叶结点
{
if((2*p+2 <= border) && (heap[2*p+1] > heap[2*p+2])) // 右孩子存在 右孩子较小
minChild = 2*p+2;
else // 右孩子不存在 或 右孩子较大
minChild = 2*p+1;
if(heap[p] <= heap[minChild]) // 若当前结点不大于其最小的孩子,结束
break;
else // 否则将p和其最小孩子交换
{
temp = heap[p] ; heap[p] = heap[minChild] ; heap[minChild] = temp;
p = minChild; // 当前下移元素的位置
}
}
}
//建堆算法
void CreateHeap(ElemType heap[], int n)
{
int i;
for(i=(n-2)/2 ; i>-1 ;i--) // 从最后一个叶结点的双亲反向到根结点
AdjustDown(heap,i,n-1); // 依次执行向下调整
}
|
优先权队列
进队
- 将新元素放堆尾,并按照最小堆(或最大堆)进行调整$O(log_2n)$
出队
- 直接取出堆顶元素$O(1)$
- 按照最小堆(或最大堆)进行适当调整$O(log_2n)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| //定义
typedef struct priorityQueue
{
ElemType *element; // 存储元素数据
int n; // 元素个数
int maxSize; // 优先队列容量
}PriorityQueue;
//创建
void CreatePQ(PriorityQueue *PQ, int mSize)
{
PQ->maxSize = mSize; // PQ最大容量赋值
PQ->n = 0; // PQ元素个数为0
PQ->element = (ElemType*)malloc(mSize*sizeof(ElemType)); // 申请空间
}
//销毁
void Destroy(PriorityQueue *PQ)
{
free(PQ->element); // 释放数组空间
PQ->n = 0; // PQ元素个数为0
PQ->maxSize = 0; // PQ容量清零
}
//释放
void Append(PriorityQueue *PQ, ElemType x)
{
if(IsFull(PQ)) //满队
return;
PQ->element[PQ->n] = x; // 优先权队列最后一个元素后面插入一个元素
PQ->n++; // 元素数量+1
AdjustUp(PQ->element, PQ->n-1); // 新增元素向上调整
}
//取出
void Serve(PriorityQueue *PQ, ElemType *x)
{
if(IsEmpty(PQ)) // 空队
return;
*x = PQ->element[0]; // 栈顶元素赋值
PQ->n--; // 元素个数-1
PQ->element[0] = PQ->element[PQ->n]; // 用堆尾替代堆顶元素
AdjustDown(PQ->element, 0, PQ->n-1); // 向上调整
}
|
哈夫曼树
扩充二叉树路径长度(不存在度为1的结点)
$$E=I+2n$$
- $I$——内路径长度根到分支结点路径和
- $E$——外路径长度根到叶子的路径长度
加权路径长度
$$WPL={\sum}_{k=1}^mw_kl_k$$
- $m$——叶结点数量
- $w_k$第$k$个叶结点权值
- $l_k$该叶结点路径长度
- $WPL$——文本最终转换成编码的总编码长度
哈夫曼树和哈夫曼编码
- 哈夫曼树是最小加权路径长度的扩充二叉树
- 分支节点权值$=$左孩子权值$+$右孩子权值
实现方法
- 选取最小的两个值
- 求和形成新的值,并与剩下的最小的求和
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| BinaryTree CreateHFMTree(int w[], int m)
{
BinaryTree x,y,z; // 二叉树变量
Create(PQ,m); // 初始化优先权队列PQ, 优先权存在根结点数据域
for(int i=0 ; i<m ; i++)
{
MakeTree(x,w[i],NULL,NULL); // 创建仅包含根结点二叉树,权值w[i]存入根结点
Append(PQ,x); // 将二叉树x插入优先权队列
}
while(PQ.n > 1)
{
Serve(PQ,x); // 从PQ中取出根结点权值最小的二叉树,存入x
Serve(PQ,y); // 从PQ中取出根结点权值最小的二叉树,存入y
}
//合并二叉树x,y
if(x.root.element < y.root.element) // 左子树结点权值小于右子树
MakeTree(z, x.root.element+x.root.element, x, y);
else
MakeTree(z, x.root.element+x.root.element, y, x);
Append(PQ, z); // 新合成新二叉树z插入优先权队列
Serve(PQ, x); // 获取优先权队列唯一二叉树,存入x,该二叉树即哈夫曼树
return x;
}
|
哈夫曼编码
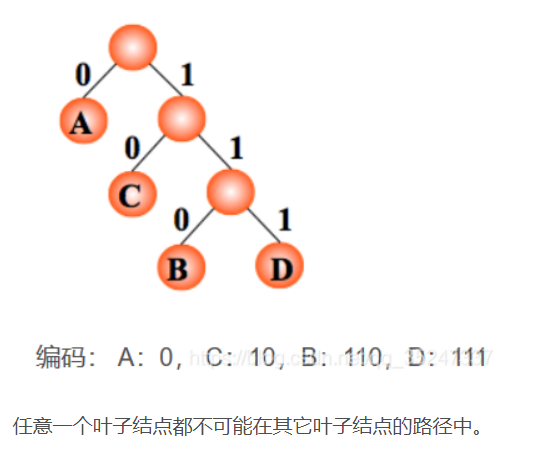
集合和搜索
集合
1
2
3
4
5
6
| typedef struct
{
int n;
int maxLength;
ElemType *element;
}ListSet;
|
顺序搜索
无序表
- 从头开始检查,将指定元素$x$与关键字比较
- 若相等搜索成功
- 若搜索完整个表,不存在,则搜索失败
1
2
3
4
5
6
7
8
| int SeqSearch(ListSet L, ElemType x)
{
int i;
for(i=0 ; i < L.n ; i++)
if(L.element[i] == x)
return i; // 搜索成功
return -1; // 搜索失败
}
|
有序表
- 关键字值满足$key_i{\leq}key_{i+1}$
- $key_i$表示$a_i$的关键字
步骤
- 从头开始检查,将指定元素$x$与关键字比较
- 若相等搜索成功
- 若某个元素关键字大于指定元素$x$,则搜索失败
无哨兵
1
| int SeqSearch(ListSet L, ElemType x){ int i; for(i=0 ; i < L.n ; i++) { if(L.element[i] == x) return i; // 搜索成功 else if(L.element[i] > x) return -1; // 搜索失败 } return -1; // 搜索失败}
|
有哨兵
1
| int SeqSearch(ListSet L, ElemType x){ int i; L.element[L.n] = MaxNum; // MaxNum正无穷 for(i=0 ; L.element[i] < x ; i++) if(L.element[i] == x) return i; // 搜索成功 return -1; // 搜索失败}
|
对半搜索
有序表$$(a_0,a_1,a_2,……,a_{n-1})$$
- 有序表长$L\leq{0}$,搜索失败
- 有序表长$L{\geq}0$,取某个元素$a_{m}$与$x$比较$m=\dfrac{low+high}{2}$,$low=0,high=n-1$
- $a_m.key = x.key$,搜索成功
- $a_m.key>x.key$,二分搜索$(a_0,a_1,a_2,…,a_{m-1})$
- $a_m.key<x.key$,二分搜索$(a_{m+1},a_{m+2},…,a_{n-1})$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| //递归
int BinSearch(ListSet L, ElemType x, int low, int high)
{
if(low <= high)
{
int m = (low+high) / 2; // 对半分割
if(x < L.element[m])
return BinSearch(L,x,low,m-1);
else if(x > L.element[m])
return BinSearch(L,x,m+1,high);
else
return m; // 搜索成功
}
return -1; // 搜索成功
}
//迭代
int BinSearch(ListSet L, ElemType x)
{
int m,kow = 0;high = L.n-1;
while(low <= high)
{
m = (low+high)/2; // 对半分割
if(x < L.element[m])
high = m-1;
else if(x > L.element[m])
low = m+1;
else
return m;
}
return -1;
}
|
搜索长度
搜索成功
搜索失败
无序表顺序搜索
$$\dfrac{n+1}{2}$$
$$n$$
有序表顺序搜索
$$\dfrac{n+1}{2}$$
$$2+{\dfrac{n}{2}}$$
对半搜索
$$S_{success}=\dfrac{2^n(n-1)+k(n+1)+1}{N}$$ $$N=2^n-1+k$$
$$S_{fail}=\dfrac{n2^n+(n+2)k}{2^n+k}$$
搜索树
二叉搜索树
- 左子树小于根结点
- 右子树大于根结点
- 若以中序遍历二叉搜索树,将得到递增有序序列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| //定义集合项
typedef struct entry
{
KeyType Key;
DataType Data;
}T
//定义结点
typedef struct btnode
{
T Element;
struct btnode *lChild, *rChild;
}BTNode;
//定义搜索树
typedef struct btree
{
BTNode *root;
}BTree;
|
查找关键字$x$
- 二叉树为空,搜索失败
- 将$x$与根结点比较
- $k$小于该结点,搜索左子树
- $k$大于该结点,搜索右子树
- $k$等于该结点,搜索成功
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| //递归
BTNode *Find(BTNode *p,KeyType k)
{
if(!p)
return NULL; // 搜索失败
if(k == p->element.key)
return p; // 搜索成功
if(k < p->element.key)
return Find(p->lChild,k);
return Find(p->rChild,k);
}
BOOL BtSearch(BTree Bt,KeyType k,T *x)
{
BTNode *p = Find(Bt.root,k);
if(p)
{
*x = p->element;
return TRUE;
}
return FALSE;
}
//迭代
BOOL BtSearch(Btree Bt,KeyType k,T *x)
{
BTNode *p = Bt.Root; // 从根结点出发
while(p)
{
if(k < p->element.key) // 从左分支继续向下搜索
p = p->lChild;
else if(k > p->element.key) // 从右分支继续向下搜索
p = p->rChild;
else
{
*x = p->element; // 搜索成功
return TRUE;
}
}
return FALSE;
}
|
插入
1
| BOOL Insert(Btree *bt, T x){ BTNode *p = bt->root, *q, *r; // p:从根节点向下搜索 q:记录搜索失败上一层结点 KeyType k = x.key; while(p) { q = p; if(k < p->element.key) p = p->lChild; else if(k > p->element.key) p = p->rChild; else return FALSE; }}
|
删除叶子结点
直接删
- 将待删除结点双亲结点指向NULL
- 释放待删除结点
删除有一个孩子结点
爷带孙
- 待删除结点的双亲结点指向待删除结点的孩子
- 释放待删除结点
删除有两个孩子结点
- 从后代选择一个覆盖待删除结点
- 保持二叉搜索树有序性==左孩子$\leq$代替这$\leq$右孩子==
- 容易删除==只有一个孩子或没有孩子==
- 删除重复的代替者
二叉平衡树
- 二叉搜索树
- 左右子树高度$h’\leq{1}$
- 左右子树都是二叉平衡树
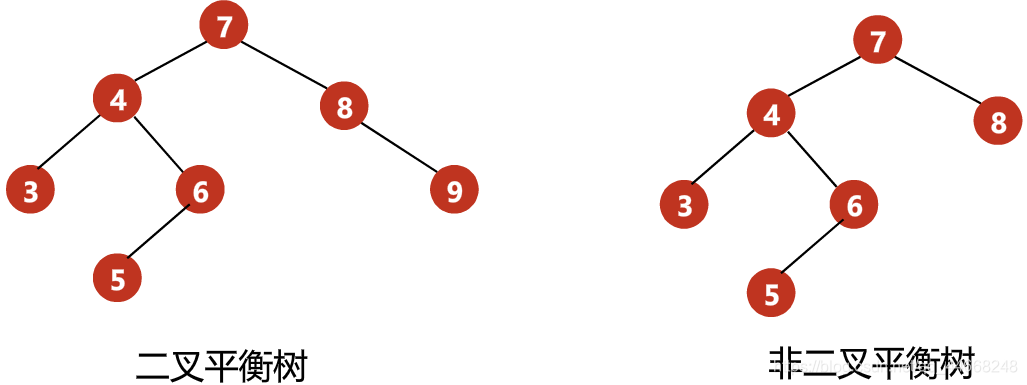
- 平衡因子——左子树与右子树高度差$h_{left}-h_{right}$
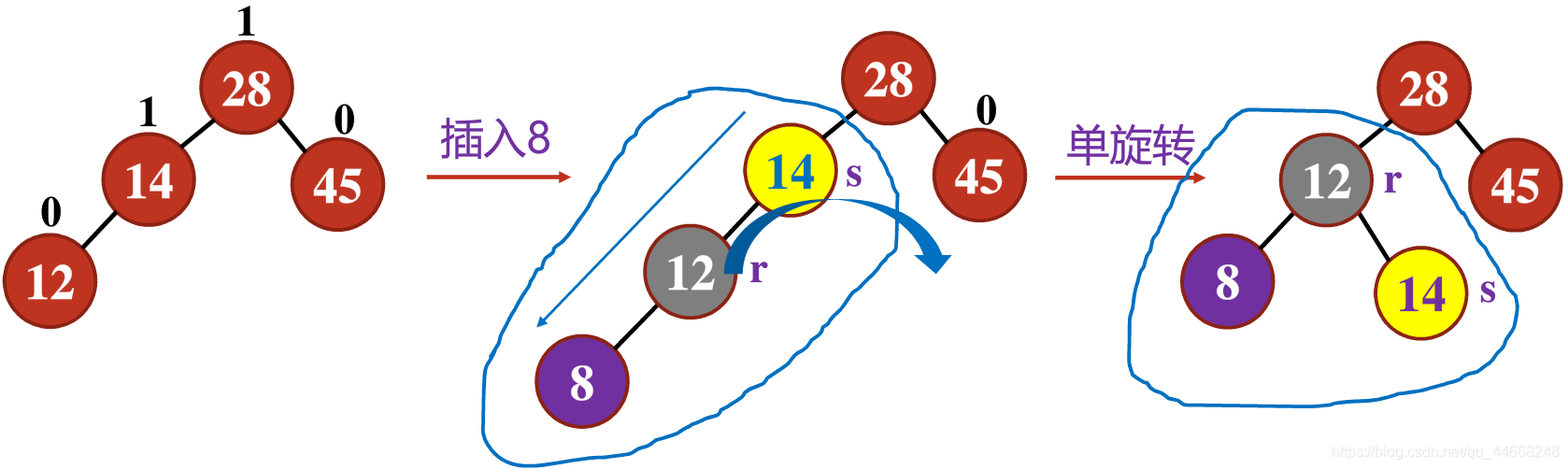
二叉平衡树插入
- 先按照普通二叉搜索树插入
- 若不平衡,则进行调整
- 先找到平衡因子超过$1$的根结点$s$
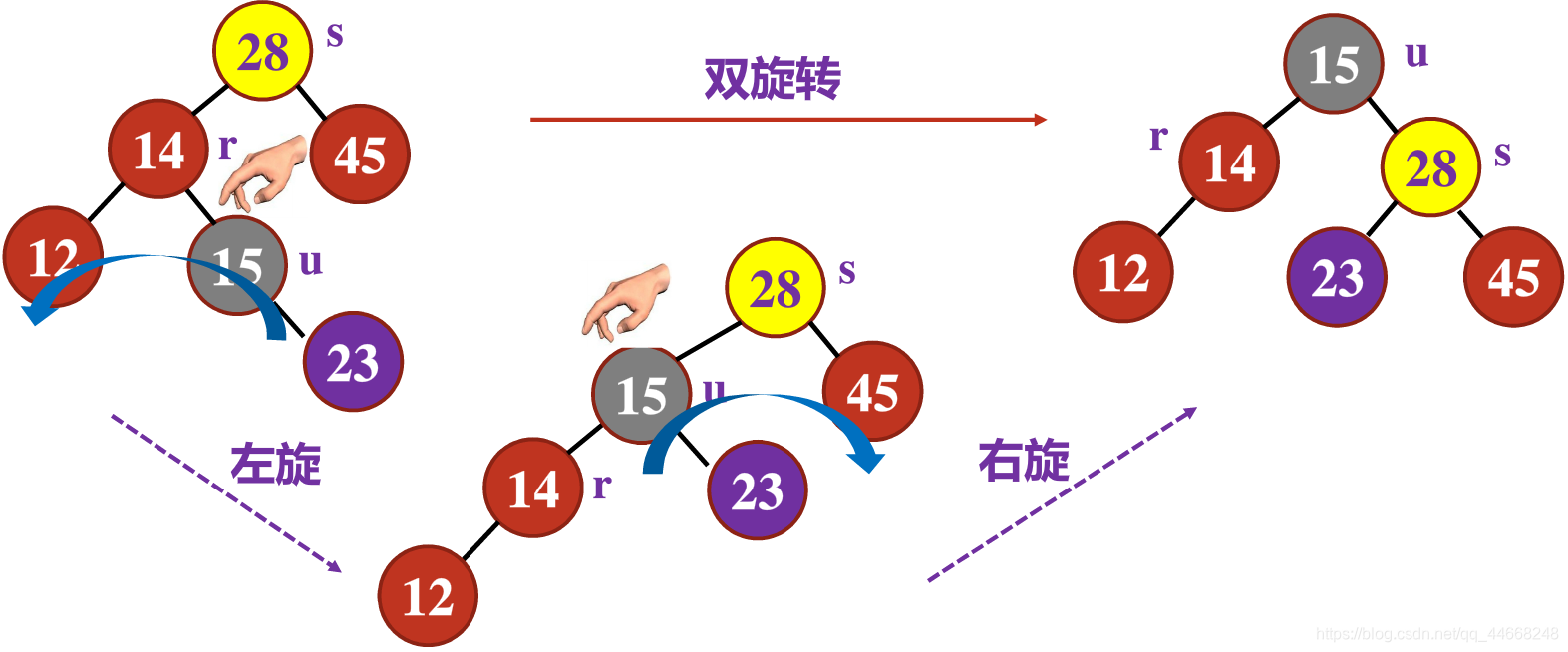
- $LL/RR$类型——单旋转新结点插入$s$的左/右结点
- $LR/RL$类型——双旋转
m叉搜索树

- 空树——失败结点
- ==失败结点不是叶子节点==
- 根结点最多$m$棵子树

- $k_i$是元素关键字
- $P_i$是指向子树的指针
- $n$为该结点元素个数,$1{\leq}n{\leq}m$
- 子树$P_i$所有关键字大于$K_i$,小于$K_{i+1}$
- 子树$P_0$所有关键字值小于$K_1$子树$P_n$上所有关键字大于$K_n$
- 子树$P_i(0{\leq}i{\leq}n)$也是$m$叉二叉树
- 结点最多存放_m-1_个元素和_m_个指针
- 结点里元素个数比包含指针少$1$
性质
- 高度为$h$的$m$二叉树最多$m^h-1$个元素高度为$h$的$m$二叉树最多$\dfrac{m^h-1}{m-1}$个结点
- 含有$N$个元素的$m$叉搜索树高度$h$满足$h{\leq}log_m(N+1)$
B-树
- 或者为空树
- 或满足$m$叉搜索树
- 根结点至少两个孩子==可以只有一个元素==
- 除根结点和失败结点所有结点**至少$\dfrac{m}{2}$**个孩子==确保B-树不会退化为单支树==
- 所有失败结点在同一层==考虑平衡性==
判定性质
- 一个结点最多$m$个孩子,$m-1$个关键字
- 除根结点与失败结点每个结点至少$\dfrac{m}{2}$个孩子,$\dfrac{m}{2}-1$个关键字
- 根结点最少2个孩子
- 失败结点均在同一层,失败结点的双亲是叶子结点
判定方法
- 失败结点是否在同一层
- 根结点是否至少$2$个孩子
- 确定$m$并计算$\dfrac{m}{2}$
- 查看除根结点与失败者外所有结点的孩子数量是否少于$\dfrac{m}{2}$
性质
- $N=s-1$$s$——失败点总数$N$——$B-$树失败点总数
- 含有$N$个元素的$m$阶$B-$树高度$h$:$h{\leq}1+log_{\frac{m}{2}}{\dfrac{N+1}{2}}$
搜索

- $B-$树中找结点,执行访问磁盘次数最多$log_{\frac{m}{2}}{\dfrac{N+1}{2}}$
- 结点中找关键字
插入

步骤
- 搜索待插入元素若已存在,则插入失败
- 插入停留的失败结点的叶子结点中
- 将结点分为{$1$
${\dfrac{m}{2}-1}$}、{$\dfrac{m}{2}$}、{${\dfrac{m}{2}}$$m$}
- 将{$\dfrac{m}{2}$}和其指针插入其双亲结点
删除
- 叶子结点直接删除
- 否则以其右子树最小元素替换

- 如发生下溢出,则若其左右兄弟有多于$\dfrac{m}{2}$个元素,则向其接一个元素

- 没有富余兄弟,与兄弟合并且将两结点之间元素下移


散列表
散列技术
散列函数($h,hash$):存储关键字($key$)和存储位置($Loc$)之间关系
- 冲突:$key_1{\neq}key_2$,$h(key_1)=h(key_2)$
- 同义词:对给定$h$,具有相同散列值不同数字
常见散列函数
除留余数法
$h(key)=key\%M$
==模值取不超过$M$的素数$P$更好==
不足
- 存在不动点$h(0)=0$,与均分布相悖
- 相邻的关键字散列到相邻地址
除留余数法改进MAD
$h(key)=(key*a+b)%P$
- $b$作为偏移量,消除了不动点
- $a$作为间隔量,原本相邻地址变成间隔$a$
平方取中法
$h(key)=(key)^2$的中间若干位
- 位数$k$满足:$10^{k-1}{\leq}n{\leq}10^k$$n$为集合中元素个数
折叠法
- 折叠法自左到右,分为位数相等几部分,每部分位数与散列表地址相同
- 将数据叠加
冲突处理技术
拉链法

时间复杂度
- 查找:$O(\dfrac{n}{M})$
- 插入:$O(\dfrac{n}{M})$
- 删除:$O(\dfrac{n}{M})$
线性探查法
解决方式
$h_i=(h(key)+i)modM$
聚集问题:线性聚集
二次探查法
解决方式
$h_{2i-1}=(h(key)+i^2)modM$
$h_{2i}=(h(key)-i^2)modM$
聚集问题:二次聚集
双散列法
解决方式
$H_{i}=(h_1(key)+ih_2(key))modM$
总结
冲突处理方法
解决方式
开/闭散列法
冲突问题
成功搜索长度
失败搜索长度
拉链法
$$/$$
开散列法
无
$$1+\dfrac{\alpha}{2}$$
$$\alpha+e^{-\alpha}$$
线性探查法
$$h_i=(h(key)+i)modM$$
开放地址法
线性聚集
$$\dfrac{1}{2}(1+\dfrac{1}{1-\alpha})$$
$$\dfrac{1}{2}(1+\dfrac{1}{(1-\alpha)^2})$$
二次探查法
$$h{2i-1}=(h(key)+i^2)modM$$ $$h{2i}=(h(key)-i^2)modM$$
开放地址法
二次聚集
$$-\dfrac{1}{\alpha}log_e(1-\alpha)$$
$$-\dfrac{1}{1-\alpha}$$
双散列法
$$H_{i}=(h_1(key)+ih_2(key))modM$$
开放地址法
$$/$$
$$-\dfrac{1}{\alpha}log_e(1-\alpha)$$
$$-\dfrac{1}{1-\alpha}$$
图
基本概念
- $G=(V,E)$
- $<u,v>$——有向图
- $(u,v)$——无向图
基本术语
- 自回路:图中存在$<u,u>$或$(u,u)$
- 多重图:两个顶点间有多条相同的边

- 完全图:图有最多的边
- 无向完全图:${\dfrac{n(n-1)}{2}}$条边
- 有向完全图:$n(n-1)$条边
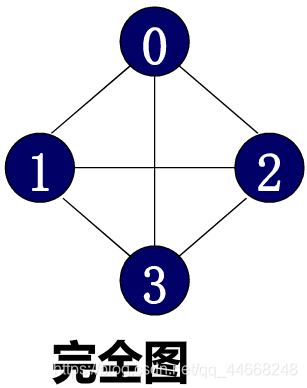
- 简单路径:除起始点,路径上其他各点都不相同
- 回路:起始点相同的简单路径
- 连通图:任两个点之间想通强连通图:最多$n(n-1)$边
- 连通分量:无向图极大连通子图
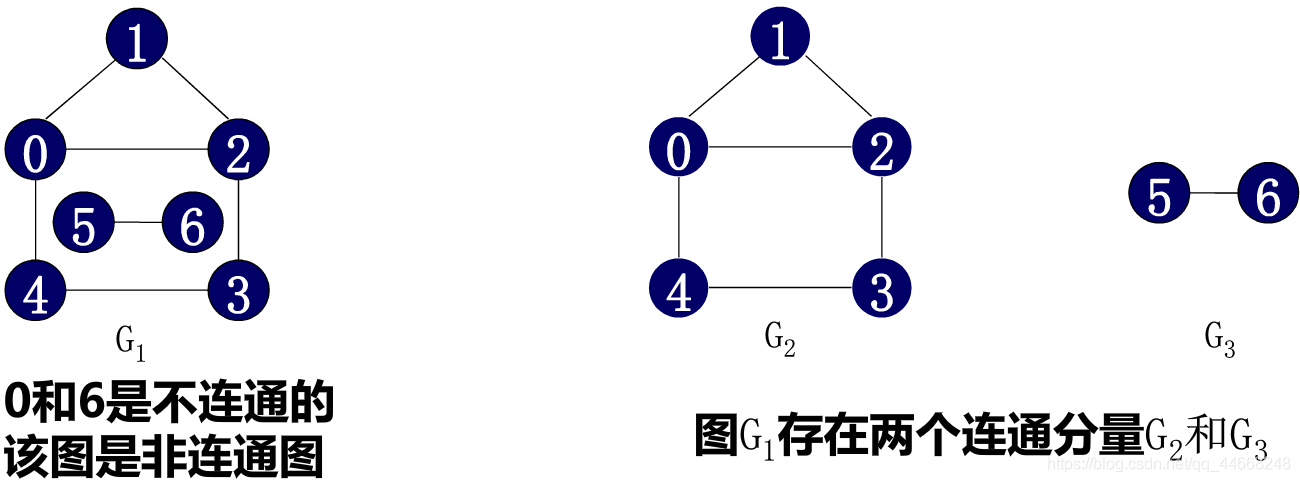
- 连通分量可能有多个
- 若加一个点,仍然连通,则非连通分量
- 顶点的度:与该顶点相关联的边的数目
- 入度:以$v$为头边的数目
- 出度:以$v$为尾边的数目
领接矩阵
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
| typedef struct mgraph
{
ElemType **a;// 动态二维数组,用来存储邻接矩阵
int n; // 图中顶点数
int e; // 图中边数
ElemType noEdge; // 两顶点无边的值
}mGraph;
//初始化
void Init(mGraph *mg, int nSize, ElemType noEdgeValue)
{
int i,j;
mg->n = nSize; // 初始化顶点数
mg->e = 0; // 初始化边数
mg->noEdge = noEdgeValue; // 初始化无边时的取值
mg->a = (ElemType**)malloc(nSize*sizeof(ElemType**)); // 数组申请空间
for(i=0; i < mg->n ;i++)
{
mg->a[i] = (ElemType*)malloc(nSize*sizeof(ElemType)); // 申请结点空间
for(j=0 ;j < mg->n ; j++)
mg->a[i][j] = mg->noEdge;
mg->a[i][i] = 0; // 回路
}
}
//销毁
void Destroy(mGraph *mg)
{
int i;
for(i=0 ; i < mg->n ; i++)
free(mg->a[i]); // 依次释放n个一维数组的存储空间
free(mg->a); // 释放以为指针数组存储空间
}
//搜索
Status Exist(mGraph *mg, int u, int v)
{
if(u<0 v<0 u > mg->n-1 v > mg->n-1 u==v) // 越界 回路
return FALSE;
else if(mg->a[u][v] != mg->noEdge) // 不为不存在的边
return True;
return False;
}
//插入
Status Insert(mGraph *mg, int u, int v, ElemType w)
{
if(u<0 v<0 u > mg->n-1 v > mg->n-1 u==v) // 越界 回路
return ERROR;
else if(mg->a[u][v] != mg->noEdge) // 插入边已存在
return Duplicate;
else
mg->a[u][v] = w; // 插入新边
mg->e++; // 边数+1
return OK;
}
//删除
Status Remove(mGraph *mg, int u, int v)
{
if(u<0 v<0 u > mg->n-1 v > mg->n-1 u==v) // 越界 回路
return ERROR;
else if(mg->a[u][v] != mg->noEdge) // 删除边不存在
return NotPresent;
else
mg->a[u][v] = mg->noEdge; // 删除边
mg->e--; // 边数+1
return OK;
}
|
优点
- 便于判断两个顶点是否有边
- 便于计算各个顶点度
- 对于无向图,第$i$行顶点之和即为顶点$i$的度
- 对于有向图,第$i$行顶点之和为顶点$i$的出度 第$i$行顶点之和为顶点$i$的入度
缺点
- 统计边的数目时间复杂度$O(n^2)$
- 空间复杂度$O(n^2)$
领接表
- 用$n$个单链表代替邻接矩阵中的$n$行
- 每个顶点对应一个单链表
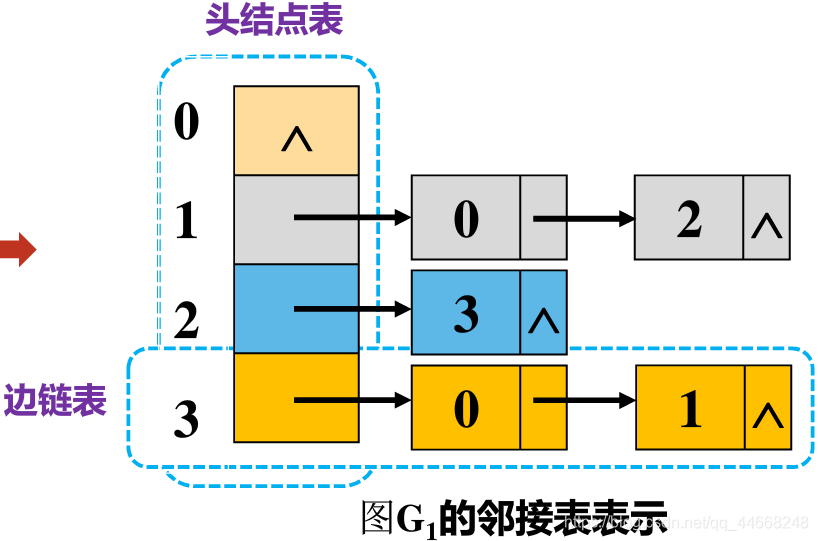
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| typedef struct eNode // 边结点定义
{
int AdjVex; // 邻接点域
ElemType w; // 权重域
struct ENode* NextArc; // 指针域
}ENode;
typedef struct lGraph
{
ENode **a; // 指向一维指针数组
int n; // 顶点数
int e; // 边数
}LGraph;
//初始化
Status Init(LGraph *lg, int nSize)
{
int i;
lg->n = nSize;
lg->e = 0;
lg->a = (ENode**)malloc(nSize*sizeof(ENode*));
if(!lg->a)
return ERROR;
else
{
for(i=0 ; i < lg->n ; i++)
lg->a[i] = NULL; // 将指针a置空
return OK;
}
}
//插入
Status Insert (LGraph *lg, int u, int v, ElemType w)
{
ENode* P;
if(u<0 v<0 u > lg->n-1 v > lg->n-1 u==v) // 输入参数无效
return Error;
if(Exist(lg,u,v)) // 边是否存在
return Duplicate;
else
p=(ENode*)malloc(sizeof(ENode));
p->adjVex = v;
p->w = w;
p->nextArc = lg->a[u];
lg->a[u] = p;
lg->e++;
return OK;
}
//删除
Status Remove(LGraph *lg, int u, int v)
{
ENode *p,*q;
if(u<0 v<0 u > lg->n-1 v > lg->n-1 u==v) // 输入参数无效
return Error;
p = lg->a[u];
q = NULL;
while(p && p->adjVex != v) // 查找待删除边是否存在
{
q = p;
p = p->nextArc;
}
if(!p)
return NotPresent;
if(q)
q->nextArc = p->nextArc;
else
lg->a[u] = p->nextArc;
free(p);
lg->e--;
return OK;
}
|
优点
- 便于统计边数$O(n+e)$
- 空间复杂度$O(n+e)$
缺点
- 不便判断顶点之间是否有边$O(n)$
- 不便于计算各个顶点度
深度优先搜索(DFS)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| void DFS(int v, int visited[], LGraph g)
{
ENode *w;
printf("%d",v); // 访问顶点v
visited[v] = 1;
for(w = g.a[v] ; w ; w = w>nextArc)
if(!visited[w->adjVex])
DFS(w->adjVex, visited, g);
}
void DFSTraverse(LGraph g)
{
int i; // 动态生成标记数组
int *visited = (int*)malloc(g.n*sizeof(int)); // 初始化标记数组
for(i=0 ; i < g.n ; i++) // 逐一检查每个顶点,若未被访问,则调用DFS
visited[i] = 0;
for(i=0 ; i < g.n ; i++)
if(!visited[i])
DFS(i, visited, g);
free(visited);
}
|
宽度优先搜索(BFS)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| void BFS(int v, int visited[], LGraph g)
{
ENode *w;
Queue q;
create(&q, g.n); // 初始化队列
visited[v]=1; // 为顶点v打上访问标记
printf("%d",v); // 访问顶点v
EnQueue(&q,v); // 将顶点v放入队列
while(!IsEmpty(&q))
{
Front(&q,&u);
DeQueue(&q); // 队首u出队
for(w = g.a[u] ; w ; w = w->nextArc) // 依序搜索u的未被访问过邻接点,访问并将其入队
if(!visited[w->adjVex])
{
visited[w->adjVex] = 1;
printf("%d",w->adjVex);
EnQueue(&q,w->adjVex);
}
}
}
void BFSTraverse(LGraph g)
{
int i; // 动态链接生成访问标记数组
int *visited = (int*)malloc(g.n*sizeof(int));
for(i=0 ; i < g.n ; i++) // 初始化标记数组
visited[i] = 0;
for(i=0 ; i < g.n ; i++) // 依次检查每个检查点
if(!visited[i]) // 若未被访问
BFS(i, visited, g);
free(visited);
}
|
拓扑排序
AOV网:有向边表示领先关系的有向无环图
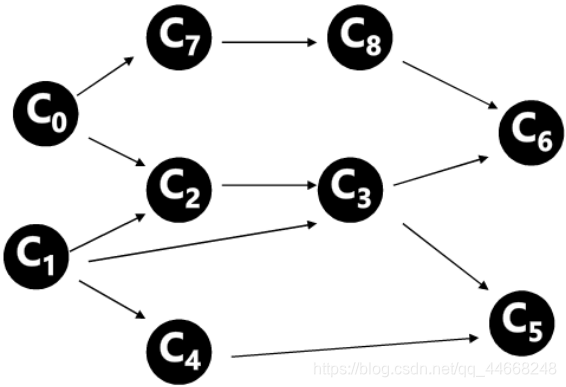
拓扑排序过程
- 找到入度$0$的点
- 删除其所有边
- 重复
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| //计算各个点的出入度
void Degree(int* inDegree, LGraph g)
{
int i;
ENode *p;
for(i=0 ; i < g.n ; i++) // 数组初始化
inDegree[i] = 0;
for(i=0 ; i < g.n ; i++)
for(p = g.a[i] ; p ; p = p->nextArc) // 检查顶点vi所有邻接点
inDegree[p->adjVex]++; // 邻接点入度+1
}
//拓扑排序
Status TopoSort(int* topo, LGraph g)
{
int i, j, k;
ENode *p;
Stack S;
int* inDegree = (int*)malloc(sizeof(int) * g.n);
Degree(inDegree, g); // 计算顶点入度
Create(&S, g.n); // 初始化栈堆
for(i=0 ; i < g.n ; i++)
if(!inDegree[i])
Push(&S, i); // 入度为0顶点入栈
while(!IsEmpty(&S)) // 若栈S不空
{
Top(&S, &i); Pop(&S); //顶点v出栈
topo[m] = i; // 将v输出到拓扑回归序列中
m++; // 对输出顶点计数
for(p=g.a[i] ; p; p = p->nextArc) // 检查顶点vi所有邻接点
{
k = p->adjVex;
inDegree[K]--; // 入度为0邻接点进栈
}
}
if(m < g.n) // 若还有顶点为输出,则表明有环
return Error;
else
return OK;
}
|
关键路径
AOE网:有向边表示持续时间的有向无环带权图

路径长度:路径上各活动持续时间的总和(即路径上所有权之和)。
完成工程的最短时间:从工程开始点(源点)到完成点(汇点)的最长路径称为完成工程的最短时间。
关键路径:路径长度最长的路径称为关键路径。
需要的四个变量:
- $E_{early}(v_i)$事件最早发生时间,顶点最早发生时间。
- $E_{late}(v_i)$事件最晚发生时间,顶点最晚发生时间。
- $A_{early}(a_k)$活动最早开始时间,边最早开始时间。
- $A_{late}(a_k)$活动最晚开始时间,边最晚开始时间。
步骤:
- 先求$E_{early}(v_i)$,从0到最后
- 再求$E_{late}(v_i)$,从最后到0
- $A_{early}(a_k)$=$E_{early}(v_i)$
- $A_{late}(a_k)$=$E_{late}(v_i)$-$w(v,j)$
- $A_{early}(a_k)$=$A_{late}(a_k)$关键顶点
- 即可确定关键路径
最小代价生成树
边权值和最小
普利姆算法(Prim)
- 分为已选$U$与未选$V$
- 选择$U$和$V$之间最小值
- 重复直到选完所有点
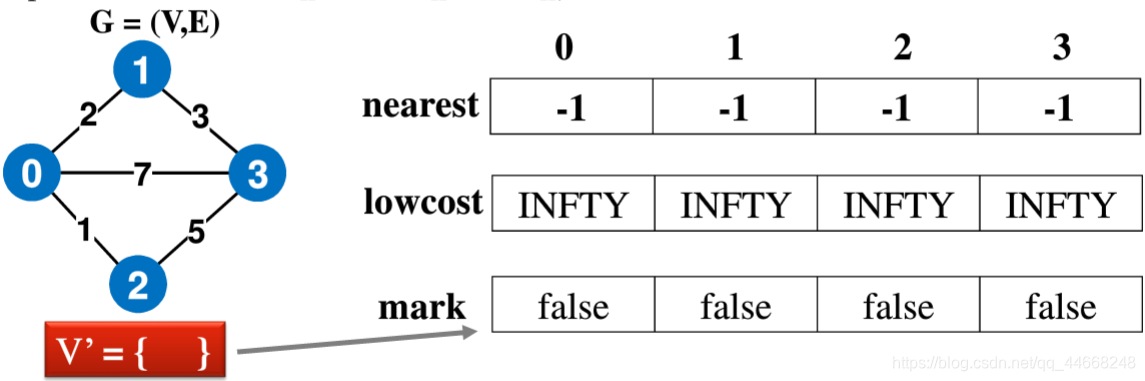
- nearst该点与未选择区域最近的点
- lowcost最短的距离
- mark是否已被选择
克鲁斯卡尔算法(Kruskal)
- 选择图中最短的边
- 若未形成回路,则继续选
- 形成了回路,再去选其他的
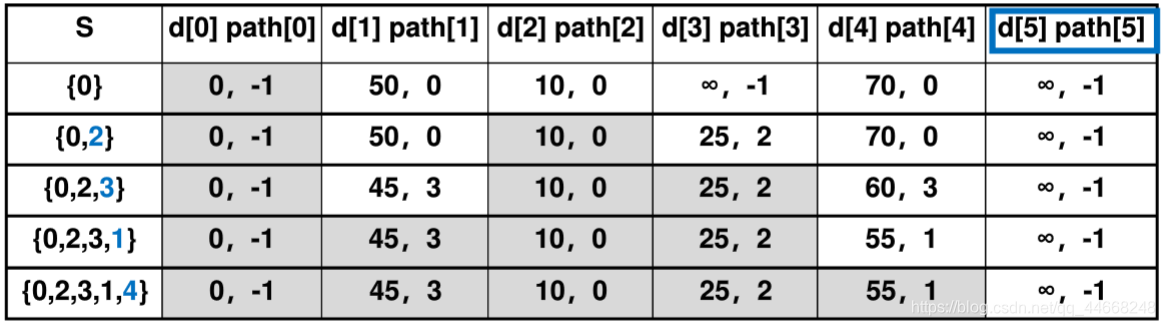
单源最短路径
迪杰斯特拉算法
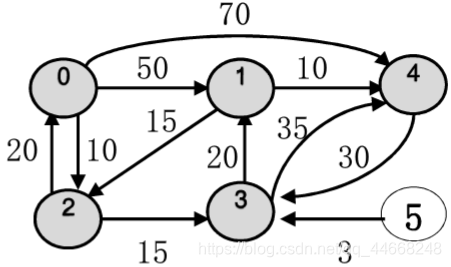
- 选已选点最短路径
- 更新${d,path}$
排序
1
2
3
4
5
6
7
8
9
10
| typedef struct entry
{
KeyType key; // 排序关键字
DataType data; // 数据项
}Entry;
typedef struct list // 顺序表
{
int n;
Entry D[MaxSize];
}List
|
选择法
1
2
3
4
5
6
7
8
9
10
| void SelectSort(List* list)
{
int minIndex,startIndex = 0;
while(startIndex < list->n-1)
{
minIndex = FindMin(*list, startIndex);
Swap(list->D, startIndex, minIndex);
startIndex++;
}
}
|
插入排序
- 前$i$元素组成有序区后$n-i-1$个元素组成无序区
- 将第$i$个元素按序插入有序区
- 以此类推

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| void InsertSort(List *list)
{
int i,j; // i标识待插入元素下标
Entry insertItem; // 每一趟待插入元素
for(i=1 ; i < list->n ; i++)
{
insertItem = list->D[i];
for(j=i-1 ; j >= 0 ; j--) // 不断将有序序列后移,为待插入元素留一个位置
{
if(insertItem.key < list->D[j].key)
list->D[j+1] = list->D[j];
else
break;
}
list->D[j+1] = insertItem; // 待插入元素有序存放至有序序列中
}
}
|
冒泡
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| void BubbleSort(List *list)
{
int i,j; // i标识每趟排序范围最后一个元素下标,每趟排序下标为0~i
BOOL isSwap = FALSE; // 标记一趟排序中是否发生了元素交换
for(i = list->n-1 ; i > 0 ; i--)
for(j = 0 ; j < i ; j++)
if(list->D[j].key > list->D[j+1].key)
{
Swap(list->D, j, j+1);
isSwap = TRUE;
}
if(!isSwap) // 若本趟排序无元素交换,排序完成
break;
}
|
快排
- 待排序序列元素数量小于1,退出
- 选择分割元素$D_s$,划分为左右子序列左子序列所有元素小于$D_s$右子序列所有元素大于$D_s$
- 子序列快速排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| int Partition(List *list, int low, int high)
{
int i = low;
int j = high+1;
Entry pivot = list->D[low]; // pivot是分割元素
do{
do
i++;
while(list->D[i].key < pivot.key && i <= high); // i前进
do
j--;
while(list->D[i].key > pivot.key && j >= low); // i前进
if(i < j)
Swap(list->D, i, j);
}while(i < j);
Swap(list->D, low, j);
return j; // j是分割元素下标
}
|
两路合并
对$[\dfrac{n}{2^{i-1}}]$个有序序列,合并$(D[0],…,D[2^{i-1}-1])$和$(D[2^{i-1}],…,D[2^{i}-1])$
- 若$[\dfrac{n}{2^{i-1}}]$是偶数,合并最后两个有序序列,否则最后一个序列不合并
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| /*子序列合并*/
void Merge(List *list, Entry *temp, int low, int n1, int n2)
{
int i =low, j = low + n1; // i,j初始时分别指向两个序列第一个元素
while( i <= low + n1 -1 && j <= low + n1 + n2 -1)
{
if(list->D[i].key <= list->D[j].key)
*temp++ = list->D[i++];
else
*temp++ = list->D[j++];
}
while(i <= low + n1 - 1)
*temp++ = list->D[i++]; // 剩余元素直接拷贝至temp
while(j <= low + n1 + n2 -1)
*temp++ = list->D[j++]; // 剩余元素直接拷贝至temp
}
void MergeSort(List *list)
{
Entry temp[MaxSize];
int low, n1, n2, i, size = 1;
while(size < list->n)
{
low = 0; // low是一对待合并序列第一个序列第一个下标
while(low + size < list->n) // 至少两个序列要合并
{
n1 = size;
if(low + size*2 < list->n)
n2 = size; // 计算第二个序列长度
else
n2 = list->n - low -size;
Merge(list, temp+low, low, n1, n2);
low += n1 + n2; // 确定下一对待合并序列中第一个序列第一个元素下标
}
for(i=0 ; i<low ; i++)
list->D[i] = temp[i]; // 复制一趟合并排序结果
size *= 2; // 子序列长度翻倍
}
}
|
堆排序
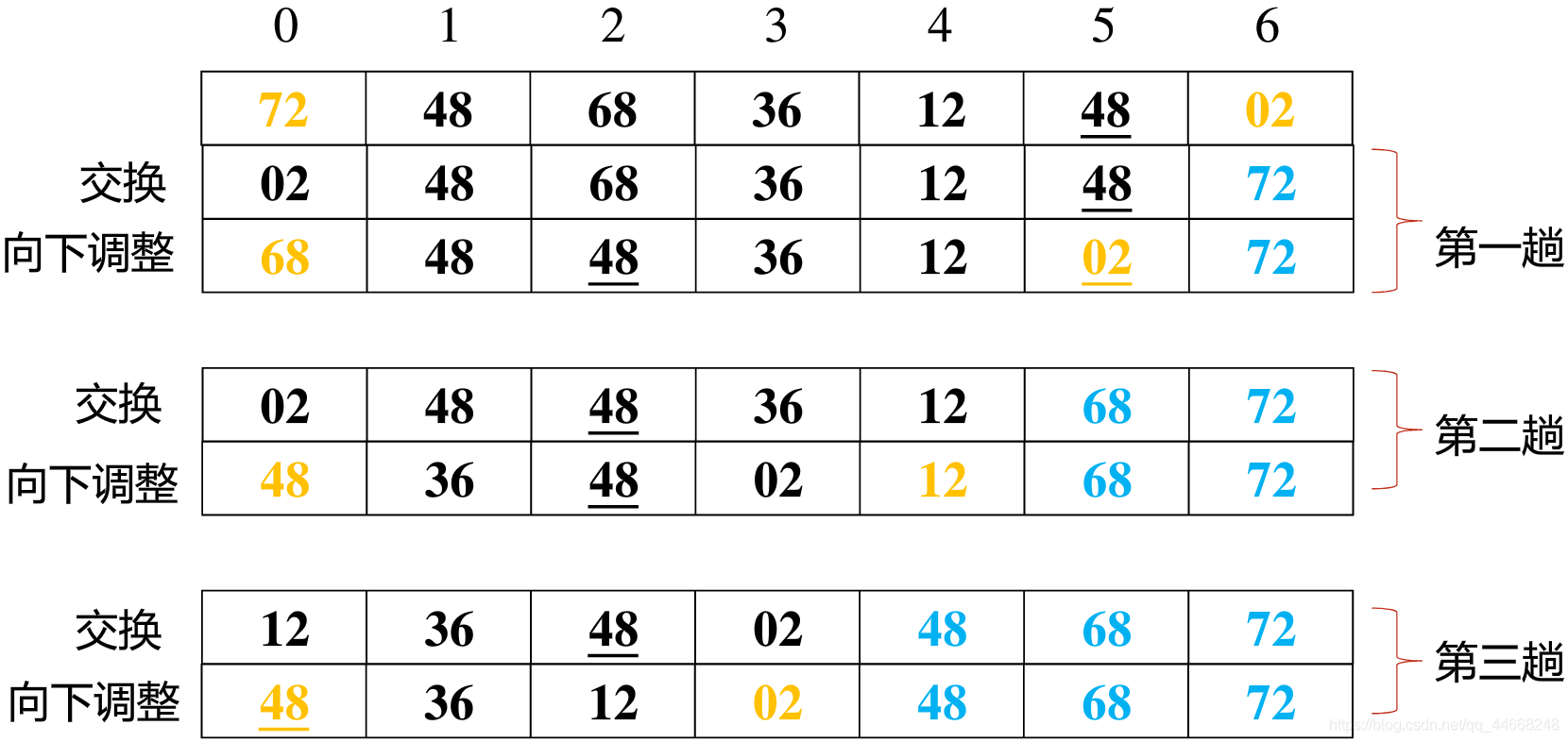
总结
排序算 法
各趟排序结果
算法的稳定性
时间复杂度(平均/最好/最坏)
适用场合
一趟排序确定元素位置
简单选择排序
$n-1$
不稳定
平均:$O(n^2)$ 最好:$O(n^2)$ 最坏:$O(n^2)$
无
√
插入排序
$n-1$
稳定
平均:$O(n^2)$ 最好:$O(n)$ 最坏:$O(n^2)$
待排序序列基本有序递增
×
冒泡排序
$1$$~$$n-1$
稳定
平均:$O(n^2)$ 最好:$O(n)$ 最坏:$O(n^2)$
基本有序且简单快速实现
√
快速排序
${\geq}n-1$
不稳定
平均:$O(nlog_2n)$ 最好:$O(log_2n)$ 最坏:$O(n^2)$
非常无序
√
合并排序
$$[log_2n]$$
稳定
平均:$O(nlog_2n)$ 最好:$O(nlog_2n)$ 最坏:$O(nlog_2n)$
多数场合,不要节省空间
×
堆排序
不稳定
平均:$O(nlog_2n)$ 最好:$O(nlog_2n)$ 最坏:$O(nlog_2n)$
√

























 各子树顺序可交换
各子树顺序可交换 各子树顺序不可交换
各子树顺序不可交换





































